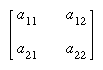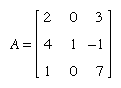http://100.daum.net/encyclopedia/view.do?docid=b24h3886a
선형 및 다(多)선형 대수학에서 n행과 n열의 정방행렬 A와 관련된 값.
det A로 쓴다. 행렬의 원소를 aij(i는 행, j는 열을 뜻함)로 쓸 때 행렬식은 n!개의 항들의 합으로 되는데 각 항은 n개의 원소들과 그들의 부호(-1)i+j들의 곱으로써 같은 행이나 열에서 2번 이상 취하지 않는다. n〓1인 경우, 행렬식 값은 한 원소 a11의 값이 된다. n〓2인 경우, 행렬은
이고 행렬식은 a11a22-a12a21이다.
더 큰 행렬식은 보통 단계별 과정, 즉 계수와 더 작은 행렬식의 곱으로 된 각 항들의 합으로 전개해 구한다. 행렬의 한 행과 한 열을 정하고 해당하는 원소 aij에 부호(-1)i+j와 i번째 행과 j번째 열을 제외한 더 작은 행렬의 행렬식 Mij를 곱한다. 이런 곱의 과정을 작은 행렬식을 구할 수 있을 때까지 확장한다. 각 단계에서 0이 가장 많은 행과 열을 택하면 계산이 용이하다. 예를 들어 행렬
의 행렬식은 둘째 열에 대해 전개하면 가장 쉬워 detA〓0·(-1)3M12+1·(-1)4M22+0·(-1)5M32〓M22〓(2·7-3·1)〓11이다.
분류
'수학 > linear algebra' 카테고리의 다른 글
| 가우스 소거법, 가우스 조던 소거법 (0) | 2012.04.16 |
|---|---|
| 소행렬식을 이용한 3x3행렬의 determinant(행렬식) (0) | 2012.04.14 |
| c언어 역행렬 구하는 함수 (1) | 2012.03.17 |
| 연립방정식을 푸는 이유는 (0) | 2012.03.16 |
| 엑셀에서 행렬곱 (0) | 2012.03.11 |