http://ko.wikipedia.org/wiki/%EA%B0%80%EC%9A%B0%EC%8A%A4_%EC%86%8C%EA%B1%B0%EB%B2%95
가우스 소거법의 과정
[편집] 전진 소거법(Forward elimination)
-
- 첫째 식의 -2배를 둘째 식에 더한다.
- 첫째 식의 1배를 셋째 식에 더한다.
-
- 둘째 식의 1배를 셋째 식에 더한다.
[편집] 후진 대입법(Backward substitution)
-
- 셋째 식이 w = 2임을 말한다.
- w를 둘째 식에 대입하여 v를 구하면 v = 1이다.
- 마찬가지로 v, w를 첫째 식에 대입하여 u를 구하면 u = 1이다.
각 식 앞에 있는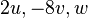 
의 계수인 2, -8, 1을 피벗(pivot)이라고 부른다.
[편집] 풀기 곤란한 경우
[편집] 정칙(Nonsingular) 행렬일 경우의 예
(식 2와 3을 바꾸어 해결한다)
[편집] 비정칙(Singular) 행렬일 경우의 예
(해가 없는 경우도 있다.)
가우스-요르단 소거법
위키백과, 우리 모두의 백과사전.
(가우스 조단 소거법에서 넘어옴)
가우스-요르단 소거법(Gauss Jordan Elimination)은 역행렬을 구하는 방법이다.
다음 예제와 같은 방법으로 풀이한다.
으로 주어진 행렬 
의 역행렬을 구하고자 하면,
![\begin{align}
\begin{bmatrix}
\ A &\vert& I \ \\
\end{bmatrix} &\rightarrow& \left[ \left. \begin{matrix}
-1 & 1 & 2 \\
3 & -1 & 1 \\
-1 & 3 & 4 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{matrix} \right] \qquad \\
&\rightarrow& \left[ \left. \begin{matrix}
-1 & 1 & 2 \\
0 & 2 & 7 \\
0 & 2 & 2 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
1 & 0 & 0 \\
3 & 1 & 0 \\
-1 & 0 & 1 \\
\end{matrix} \right] \qquad \\
&\rightarrow& \left[ \left. \begin{matrix}
-1 & 1 & 2 \\
0 & 2 & 7 \\
0 & 0 & -5 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
1 & 0 & 0 \\
3 & 1 & 0 \\
-4 & -1 & 1 \\
\end{matrix} \right]
\end{align}](http://upload.wikimedia.org/wikipedia/ko/math/f/b/3/fb30fe1cc258793a3095a9287505ec83.png)
이 된다. 이것은 가우스 소거법에 의한 방법이다. 가우스-요르단 연산 절차에 따라 다음과 같이 변형한다. 주대각선의 원소가 모두 1이 되는 대각행렬로 변형한다.
![\begin{align}
&& \left[ \left. \begin{matrix}
1 & -1 & -2 \\
0 & 1 & 3.5 \\
0 & 0 & 1 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
-1 & 0 & 0 \\
1.5 & 0.5 & 0 \\
0.8 & 0.2 & -0.2 \\
\end{matrix} \right] \qquad\qquad \\
&& \quad \rightarrow \left[ \left. \begin{matrix}
1 & -1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
0.6 & 0.4 & -0.4 \\
-1.3 & -0.2 & 0.7 \\
0.8 & 0.2 & -0.2 \\
\end{matrix} \right] \\
&& \quad \rightarrow \left[ \left. \begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{matrix} \ \ \right| \ \ \begin{matrix}
-0.7 & 0.2 & 0.3 \\
-1.3 & -0.2 & 0.7 \\
0.8 & 0.2 & -0.2 \\
\end{matrix} \right] \quad
\end{align}](http://upload.wikimedia.org/wikipedia/ko/math/e/f/d/efd624f339b2369ffc04e641022273a5.png)
![A^{-1}=\left[ \begin{matrix}
-0.7 & 0.2 & 0.3 \\
-1.3 & -0.2 & 0.7 \\
0.8 & 0.2 & -0.2 \\
\end{matrix} \right]](http://upload.wikimedia.org/wikipedia/ko/math/5/5/d/55da4aef5d57c54d612359f78c3dd96f.png)
이 소거법의 이름은 카를 프리드리히 가우스와 빌헬름 요르단에서 따온 것이다.